k-mean Clustering

들어가기

클러스터링(Clustering, 이하 군집화)은 데이터 내의 패턴과 구조를 식별하는 데 유용한 분석 방법으로 비지도 학습의 한 형태이다. 데이터 포인트 간의 유사성을 기반으로 데이터를 그룹화하고 특성을 발견하는 목적으로 사용된다. 군집화는 고객 데이터에서 고유한 그룹을 식별하여 세분화된 맞춤형 마케팅 전략을 수립하거나, 소셜 네트워크를 분석하여 커뮤니티 또는 그룹을 탐지하고, 예상동작과 일치하지 않는 비정상적 패턴을 식별하는 데 사용하기도 한다.

군집화 방법에는 k-mean 군집화, 계층적(Hierarchical) 군집화, 분포 군집화 등 다양한 방법이 있으나, 여기서는 와인 데이터를 k-mean 방법으로 군집화 하는 일련의 과정을 설명한다. k-mean 군집화는 각 군집 내의 분산을 최소화하여 데이터를 k개의 고유하고 겹치지 않는 하위 군집으로 분할한다.

# 필요한 라이브러리 로드   
library(tidyverse)
library(corrplot)
library(gridExtra)
library(GGally)
library(knitr)

# 데이터 읽기  
setwd("C:\\BigdataClass")
wines <- read.csv("Wine_for_clustering.csv")

데이터의 특성을 살펴보기 위해 몇개 행을 살펴보자.

# First rows 
kable(head(wines))

Alcohol	Malic_Acid	Ash	Ash_Alcanity	Magnesium	Total_Phenols	Flavanoids	Nonflavanoid_Phenols	Proanthocyanins	Color_Intensity	Hue	OD280	Proline	Customer_Segment
14.23	1.71	2.43	15.6	127	2.80	3.06	0.28	2.29	5.64	1.04	3.92	1065	1
13.20	1.78	2.14	11.2	100	2.65	2.76	0.26	1.28	4.38	1.05	3.40	1050	1
13.16	2.36	2.67	18.6	101	2.80	3.24	0.30	2.81	5.68	1.03	3.17	1185	1
14.37	1.95	2.50	16.8	113	3.85	3.49	0.24	2.18	7.80	0.86	3.45	1480	1
13.24	2.59	2.87	21.0	118	2.80	2.69	0.39	1.82	4.32	1.04	2.93	735	1
14.20	1.76	2.45	15.2	112	3.27	3.39	0.34	1.97	6.75	1.05	2.85	1450	1

#str(wines) 

데이터를 살펴보면 맨 마지막 컬럼이 Customer_Segment로 고객이 구분한 와인 구분 변수가 있다. 우리는 군집화를 통해 군집화 시킬 것이기 때문에 이 변수는 불필요하므로 군집화 시에는 삭제한다.

#  Customer_Segment 제거  
wines <- wines[, -14]

데이터의 요약 통계량을 살펴보자.

# Summary
kable(summary(wines))

	Alcohol	Malic_Acid	Ash	Ash_Alcanity	Magnesium	Total_Phenols	Flavanoids	Nonflavanoid_Phenols	Proanthocyanins	Color_Intensity	Hue	OD280	Proline
	Min. :11.03	Min. :0.740	Min. :1.360	Min. :10.60	Min. : 70.00	Min. :0.980	Min. :0.340	Min. :0.1300	Min. :0.410	Min. : 1.280	Min. :0.4800	Min. :1.270	Min. : 278.0
	1st Qu.:12.36	1st Qu.:1.603	1st Qu.:2.210	1st Qu.:17.20	1st Qu.: 88.00	1st Qu.:1.742	1st Qu.:1.205	1st Qu.:0.2700	1st Qu.:1.250	1st Qu.: 3.220	1st Qu.:0.7825	1st Qu.:1.938	1st Qu.: 500.5
	Median :13.05	Median :1.865	Median :2.360	Median :19.50	Median : 98.00	Median :2.355	Median :2.135	Median :0.3400	Median :1.555	Median : 4.690	Median :0.9650	Median :2.780	Median : 673.5
	Mean :13.00	Mean :2.336	Mean :2.367	Mean :19.49	Mean : 99.74	Mean :2.295	Mean :2.029	Mean :0.3619	Mean :1.591	Mean : 5.058	Mean :0.9574	Mean :2.612	Mean : 746.9
	3rd Qu.:13.68	3rd Qu.:3.083	3rd Qu.:2.558	3rd Qu.:21.50	3rd Qu.:107.00	3rd Qu.:2.800	3rd Qu.:2.875	3rd Qu.:0.4375	3rd Qu.:1.950	3rd Qu.: 6.200	3rd Qu.:1.1200	3rd Qu.:3.170	3rd Qu.: 985.0
	Max. :14.83	Max. :5.800	Max. :3.230	Max. :30.00	Max. :162.00	Max. :3.880	Max. :5.080	Max. :0.6600	Max. :3.580	Max. :13.000	Max. :1.7100	Max. :4.000	Max. :1680.0

Data analysis

분석에 앞서 데이터를 가시화 시켜 살펴보자. 먼저 변수별 데이터의 분포를 살펴보자.

# Histogram for each Attribute
wines %>%
  pivot_longer(cols = c(1:13), names_to = "Attributes", values_to ="value")  %>% 
#  gather(Attributes, value, 1:13) %>%          # long form으로 변환  
  ggplot(aes(x=value, fill=Attributes)) +      # Attributes별로 분포 보기  
  geom_histogram(colour="black", show.legend=FALSE) +
  facet_wrap(~Attributes, scales="free_x") +
  labs(x="Values", y="Frequency",
       title="와인의 변수별 분포(히스토그램)") +
  theme_bw()

이번에는 box_Plot으로 변수들의 분포를 가시화 시켜보자.

# Boxplot for each Attribute  
wines %>%
  pivot_longer(cols = c(1:13), names_to = "Attributes", values_to ="value")  %>%   
  ggplot(aes(x=Attributes, y=value, fill=Attributes)) +
  geom_boxplot(show.legend=FALSE) +
  labs(title="와인의 변수별 분포(박스플롯)") +
  theme_bw() +
  theme(axis.title.y=element_blank(),
        axis.title.x=element_blank()) +
  coord_flip()

그림이 보기 좋지 않다. 여기에는 두가지 이유가 있다.
첫째, 다른 변수에 비해 값이 지나치게 큰 두개의 변수(Magnesium 와 Proline)로 인해 나머지 변수들은 구분이 안될 정도로 떡이 져서 데이터를 가시화한 이유가 없어졌다. 둘째, 크기 순으로 정리되어 있지 않아 보기에 아름답지 않다. 이 두가지를 개선하기 위해 하나의 그래프 안에 표현하기 힘든 변수 두개는 제거하고 reorder()함수를 이용하여 그래프 출력의 순서를 조정한다.

# Boxplot for each Attribute  
wines %>%
  pivot_longer(cols = c(1:4, 6:12), names_to ="Attributes", values_to = "value")  %>% 
  ggplot(aes(x=reorder(Attributes, value), y=value, fill=Attributes)) +
  geom_boxplot(show.legend=FALSE) +
  labs(title="와인의 변수별 분포(박스플롯)") +
  theme_bw() +
  theme(axis.title.y=element_blank(),
        axis.title.x=element_blank()) +
  coord_flip()

변수들이 크기순으로 정렬되고, 과도하게 큰 변수들을 제거하여 읽기 쉬운 Box_Plot이 되었다.

이번에는 변수간 상관관계를 가시화 시켜 살펴보자.

# Correlation matrix 
cormat <- cor(wines)
corrplot(cormat, type="upper", method="ellipse", tl.cex=0.9)

Data preparation

데이터를 k-mean 알고리즘에 적용하기 전에 고려해야 할 사항이 있다. k-mean 알고리즘 뿐만 아니라, 거리기반 알고리즘 즉 군집화 알고리즘이나, knn 등은 변수의 변동의 범위에 차이가 크게 날 경우 지배적인 일부 변수의 영향이 커져 나머지 변수의 영향력이 미약하게 될 가능성이 있다. 이런 경우에는 데이터의 척도가 같아지도록 데이터를 변환시킬 필요가 있다. 이런 방법에는 노말라이즈, 표준화 스케일 등의 방법이 있다. 여기서는 데이터를 정규화 시켜 변수의 범위를 0과 1사이로 조정한다. 이에 대한 자세한 설명은 필자의 데이터 전처리 관련 글을 참조(https://shines39.tistory.com/entry/Data-Preprocessing-I) 하면된다.

# Normalization
normalize <- function(x) { 
  return ((x - min(x)) / (max(x) - min(x)))
}
  
winesNorm <- as.data.frame(normalize(wines))

# Original data
original_p <- ggplot(wines, aes(x=Alcohol, y=Malic_Acid)) +
  geom_point() +
  labs(title="원래 데이터") +
  theme_bw()

# Normalized data 
normalize_p <- ggplot(winesNorm, aes(x=Alcohol, y=Malic_Acid)) +
  geom_point() +
  labs(title="정규화 후 데이터") +
  theme_bw()

# Subplot
grid.arrange(original_p, normalize_p, ncol=2)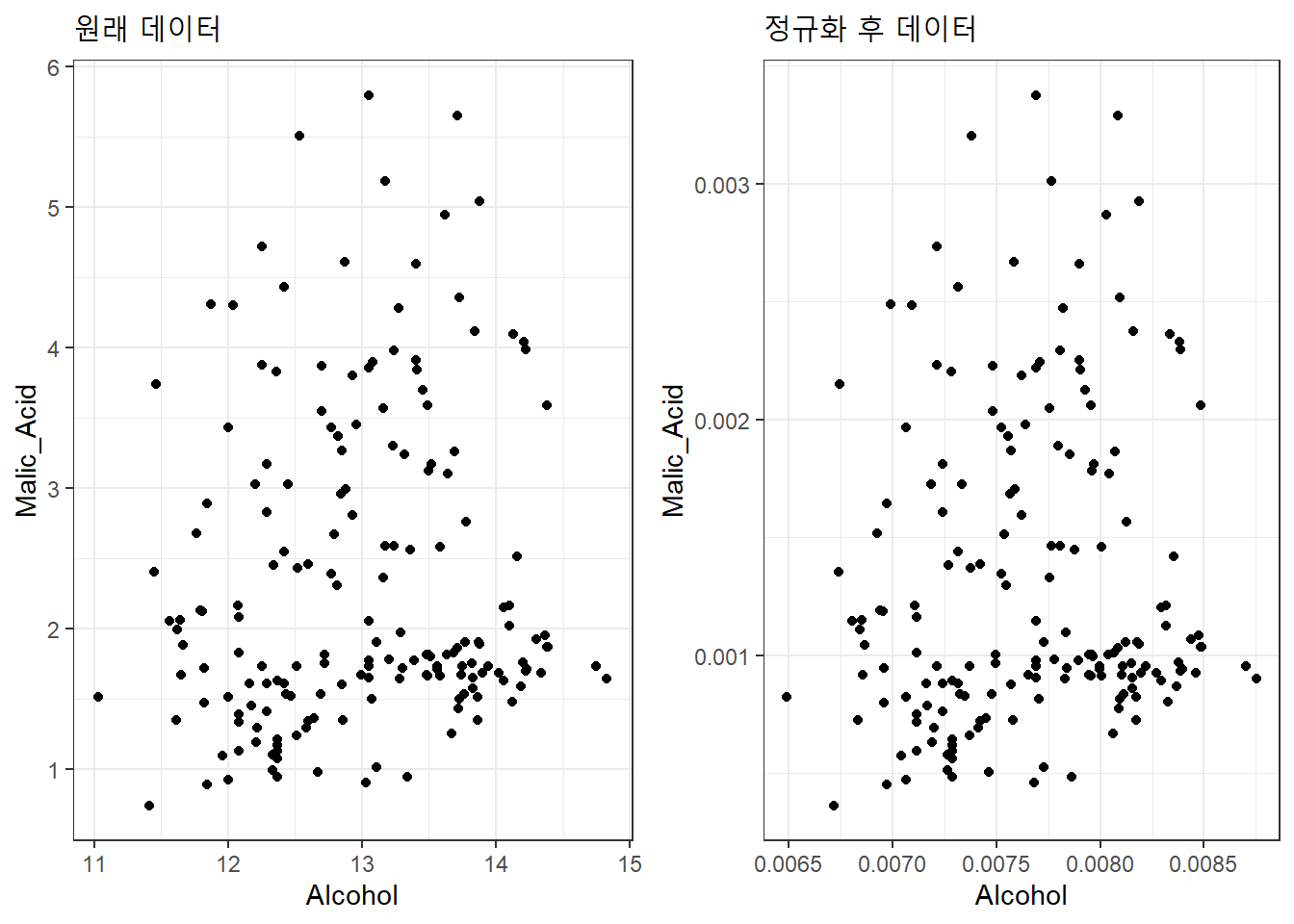

원래 데이터와 정규화 이후 데이터의 산점도는 차이가 없다. 다만 산점도 축의 척도가 달라졌을 뿐이다.

k-mean 군집화

이제 데이터가 준비가 되었으니, k-mean 군집화를 해보자. k-mean 군집은 먼저 군집수 k 값을 정해주어야 한다. 일단 k = 2로 하여 두개의 군집으로 군집을 해보자. k-means 군집을 수행하는 함수는 kmean()이다. 군집수 k는 centers 파라마터로 지정한다. kmeans() 함수는 지정한 방법으로 군집화를 수행한 후 “kmeans” 객체를 반환한다.

#  두개의 군집(k=2)으로 군집화 
set.seed(1234)
wines_k2 <- kmeans(winesNorm, centers=2)

두개의 집단으로 군집화한 결과가 들어있는 wines_k2 객체를 살펴보자.

class(wines_k2)

[1] "kmeans"

str(wines_k2)

List of 9
 $ cluster     : int [1:178] 1 1 1 1 2 1 1 1 1 1 ...
 $ centers     : num [1:2, 1:13] 0.00806 0.00748 0.00104 0.00144 0.00137 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : chr [1:2] "1" "2"
  .. ..$ : chr [1:13] "Alcohol" "Malic_Acid" "Ash" "Ash_Alcanity" ...
 $ totss       : num 6.23
 $ withinss    : num [1:2] 0.701 0.909
 $ tot.withinss: num 1.61
 $ betweenss   : num 4.62
 $ size        : int [1:2] 55 123
 $ iter        : int 1
 $ ifault      : int 0
 - attr(*, "class")= chr "kmeans"

군집결과 wines_k2는 kmeans 클래스이고 9종의 정보를 가지고 있는 리스트임을 알 수 있다. 중요한 몇가지만 살펴보자. 먼저 군집 자체의 정보를 제공하는 정보가 있다. 이것은 각 관측치(행)이 어느 클러스터에 속하는지, 각 클러스터의 중심은 어떻게 되는 지, 각각의 클러스터에 속한 관측치는 몇 개나 되는지의 정보를 담고 있다.

• cluster : 해당 관측치(행)이 속한 클러스터를 번호로 제시
• center : 각 클러스터별 변수의 중앙값을 나타내는 매트릭스
• size : 각 글러스터에 할당된 관측치의 수

# Cluster to which each point is allocated
wines_k2$cluster

  [1] 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 1 1 2 2 1 1 1 1 1 1 1 1 1 1 1
 [38] 1 1 2 2 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 1 2 2 1
 [75] 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[112] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[149] 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2

# Cluster centers
wines_k2$centers

      Alcohol  Malic_Acid         Ash Ash_Alcanity  Magnesium Total_Phenols
1 0.008058091 0.001036227 0.001367855   0.01031195 0.06319591   0.001599041
2 0.007484416 0.001437345 0.001315046   0.01207125 0.05755386   0.001150157
    Flavanoids Nonflavanoid_Phenols Proanthocyanins Color_Intensity
1 0.0016468807          9.69772e-05    0.0010518130     0.003208798
2 0.0008997502          1.56371e-04    0.0007881949     0.002810564
           Hue       OD280   Proline
1 0.0005575756 0.001748187 0.6855276
2 0.0004634989 0.001356183 0.3367760

# Cluster size
wines_k2$size

[1]  55 123

아래 정보는 군집이 어느 정도 잘 되었는지를 가늠해 볼 수 있는 정보이다. 즉 군집이 잘 되었다면 같은 군집의 데이터는 밀접하게 모여있고 군집간에는 거리가 이격되어 있을 것이라는 직관을 확인해 볼 수 있는 정보들이다.

• betweenss : 군집 간 거리의 제곱합. 좋은 군집화란 군집간 거리가 클 수록 좋음
• withinss : 군집 내 거리의 제곱합, 군집수와 같겠지. 이값은 작을 수록 군집의 응집도가 좋다는 것을 의미
• tot.withinss. 군집 내 총 거리의 제곱합

# Between-cluster sum of squares
wines_k2$betweenss

[1] 4.623925

# Within-cluster sum of squares
wines_k2$withinss

[1] 0.7008319 0.9093059

# Total within-cluster sum of squares 
wines_k2$tot.withinss

[1] 1.610138

# Total sum of squares
wines_k2$totss

[1] 6.234063

지금까지 kmeans 수행결과에 대한 각각의 정보를 알아보았다. 하지만 이 모든것이 군집수를 2(k=2)로 했을 때의 정보이다. 만일 군집을 3, 4, 5, 10 등 다양하겠 했을때 위 척도들이 어떻게 변화는 지를 살펴 보아야 최선의 군집화를 위한 군집의 수를 결졍할 수 있다. 그럼 군집수를 변화 시켜가면서 위의 지표들이 어떻게 변하는지 알아보자.

군집 수의 결정

군집의 수를 결정하기 위해서는 군집의 갯수가 변함에 따라 위에서 평가했던 지표가 어떻게 변화는 지 가시화 시켜서 눈으로 확인하는 석이 유리하다. 여기서는 군집간 거리제곱합과 군집내 총거리제곱합이 군집의 수가 변함에 따라 어떻게 변화는 지 알아보자.

bss <- numeric()
wss <- numeric()

# Run the algorithm for different values of k 
set.seed(1234)

for(i in 1:10){

  # For each k, calculate betweenss and tot.withinss
  bss[i] <- kmeans(winesNorm, centers=i)$betweenss
  wss[i] <- kmeans(winesNorm, centers=i)$tot.withinss

}

# Between-cluster sum of squares vs Choice of k
p3 <- qplot(1:10, bss, geom=c("point", "line"), 
            xlab="Number of clusters", ylab="Between-cluster sum of squares") +
  scale_x_continuous(breaks=seq(0, 10, 1)) +
  theme_bw()

## Warning: `qplot()` was deprecated in ggplot2 3.4.0.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.

# Total within-cluster sum of squares vs Choice of k
p4 <- qplot(1:10, wss, geom=c("point", "line"),
            xlab="Number of clusters", ylab="Total within-cluster sum of squares") +
  scale_x_continuous(breaks=seq(0, 10, 1)) +
  theme_bw()

# Subplot
grid.arrange(p3, p4, ncol=2)

위 그래프로 판단해 볼때, 군집을 몇개로 하는것이 최적의 군집일까? 통상 이런 형태의 그래프에서는 그래프가 급격하게 변하는 변곡점(엘보우포인트)을 선택한다. 좌측과 우측의 그래프에서는 k=3 일때 군집간 거리(거리제곱합)의 변화, 군집내 거리변화가 급격하게 변하는 엘보우포인트 임을 알수있다. 이제 최적의 군집수를 3으로 설정하고 다시 군집화를 진행해보자.

군집결과 (k=3)

k 값을 3으로 하여 kmeans()함수를 실행하면 3개의 군집으로 군집화한다. 군집 결과는 위의 k=2 경우와 같이 확인할수 있다. 여기서는 생략한다.

# Execution of k-means with k=3
set.seed(1234)

wines_k3 <- kmeans(winesNorm, centers=3)

#wines_k3$size
#wines_k3$centers   

군집의 결과를 변수 쌍으로 하여 산점도로 그리고 색깔로 군집을 구분한 그래프를 작성해보자.

# Clustering 
ggpairs(cbind(wines, Cluster=as.factor(wines_k3$cluster)),
        columns=1:12, aes(colour=Cluster, alpha=0.5),
        lower=list(continuous="points"),
        upper=list(continuous="blank"),
        axisLabels="none", switch="both") +
        theme_bw()

결론 및 요약

우리는 wine 데이터를 가지고 k-mean 군집화하는 과정을 살펴보았다. k-mean 군집화는 군집의 수가 알려져 있는 경우와 군집의 크기와 모양이 상대적으로 비슷한 대규모 데이터 세트에 유리하다. k-mean 군집화 외 계층적 군집화(Hierarchical clustering) 등의 방법도 있다.